Principio multiplicativo

Si una operación es descrita mediante una secuencia de $k$ pasos, donde:

• El número de caminos para realizar el primer paso es de $n_1$
• El número de caminos para el segundo paso es de $n_2$
• De manera sucesiva $n_r$ es el números de caminos para el $k$-ésimo paso

Entonces, el total de caminos que completan la operación es \begin{align}\prod_{i=1}^k n_i= n_1n_2\cdots n_k\end{align}

Fig. 1 Diagrama de árbol

Ejemplo 1 (Cartas) De cuantas formas se pueden escoger teniendo en cuenta el orden, 4 cartas de una baraja española. Como se puede apreciar en la Fig. 2 hay 48 cartas, por tanto, la primera carta tiene 48 formas posibles de ser escogida, la segunda tiene 47, la tercera 46 y la cuarta carta de 45 formas. Entonces, el número de maneras en que se pueden escoger las cuatro cartas es de:  $48\times 47\times 46\times 45=4.669.920$.

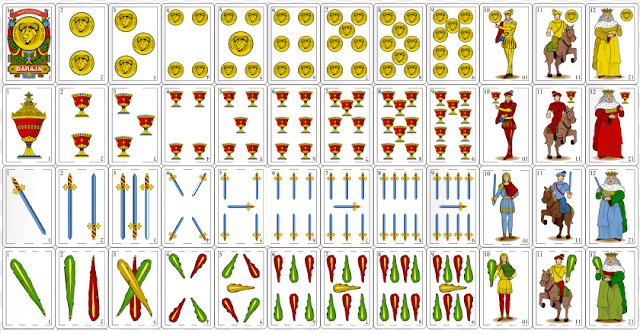
Fig. 2 Baraja española

Ejemplo 2 (Dados) Considere el experimento en lanzar dos dados y observar las caras que quedan hacia arriba. El primer dado puede caer de $6$ maneras diferentes {⚀, ⚁, ⚂, ⚃, ⚄ y ⚅} y el segundo dado también puede caer de $6$ maneras diferentes. Entonces, el número de maneras en que pueden caer ambos dados simultáneamente es:  $6\times 6=36$. Tal como se puede apreciar en la Fig. 3.

Fig. 3 Resultado de lazar dos dados

Ejemplo 3 (Dominó) De cuantas formas se pueden escoger teniendo en cuenta el orden, 4 fichas de un dominó doble seis. Como se puede apreciar en la Fig. 3 hay 28 fichas, por tanto, la primera ficha tiene 28 formas posibles de ser escogida, la segunda tiene 27, la tercera 26 y la cuarta ficha de 45 formas. Entonces, el número de maneras en que se pueden escoger las cuatro fichas es de:  $28\times 27\times 26\times 25=491.400$.

Fig. 4 Fichas del dominó doble seis.

Ejemplo 4 (Placas) Las placas para automóvil en el D. F. están formadas por $6$ caracteres: los tres primeros son dígitos y los tres últimos son letras del alfabeto. ¿Cuántas placas diferentes se pueden hacer?

Primero vamos a analizar los dígitos: el primero se puede escoger de $10$ maneras diferentes, el segundo de $10$ maneras y el tercero de $10$ maneras; así que, el número de maneras en que se puede formar la primera parte de la placa es: $10\times 10\times 10 = 1000$. Ahora bien, si se considera que el arreglo $000$ no es válido, entonces habrá que restarle $1$ al valor obtenido, con lo que quedan $999$ maneras en que se puede formar la primera parte de la placa.

Fig. 5 Placa Mexicana

La segunda parte de la placa se forma con tres letras: la primera se puede escoger de $26$ maneras diferentes (A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z), la segunda de $26$ maneras y la tercera de $26$ maneras; así que el número de maneras en que se puede formar la segunda parte de la placa es: $26\times 26\times 26 = 17.576$. Finalmente, el número total de placas diferentes que se pueden formar es: $999 \times 17.576 = 17’558.424$.