Box plot

Un boxplot es un tipo de gráfico que se utiliza para representar y comparar la distribución de un conjunto de datos numéricos. Muestra la media, la mediana, los cuartiles y los valores atípicos de los datos en una sola representación visual.

Sirve para identificar la forma de la distribución de los datos, identificar valores atípicos y comparar la distribución de varios conjuntos de datos. Es una herramienta útil para la exploración de datos y la identificación de patrones.

1. Medidas resúmenes

Son útiles para comparar conjuntos de datos numéricos y presentar resultados de un estudio estadístico. Se clasifican en cuatro grupos principales:

• Medidas de posición: Dividen un conjunto ordenado de datos en grupos de la misma cardinalidad. Percentiles, cuartiles,...
• Medidas de Centralización: Dan los puntos centrales de la distribución poblacional. (Media, mediana y moda).
• Medidas de dispersión: Pretenden expresar cuan variable es un conjunto de datos con respecto a las medidas de centralización. (Varianza, rango intercuartilico).
• Medidas de forma: Comparan la forma de la representación gráfica, bien sea el histograma o el diagrama de barras de la distribución muestral, con la curva normal. (Asimetría y curtosis).

2. Percentiles

El percentil $p\%$ de una distribución muestral o poblacional de un conjunto de datos ordenados es la observación que deja a lo sumo $p\%$ de las observaciones por debajo de él y a lo sumo $(1-p)\%$ por encima.

Fig 1. Cuartiles

Los percentiles más frecuentes son los cuartiles, es decir; los que dividen la muestra en cuatro partes iguales y corresponden a:

$$Q_1=p_{_{25}}\,,\quad mediana=p_{_{50}}\quad \text{y}\quad Q_3=p_{_{75}}$$

Estos se calculan de la siguiente forma

• El cuartil inferior ocupa la menor posición que supere o iguale el valor de $\frac{1}{4}n$ de los datos ordenados.
• La mediana ocupa la menor posición que supere o iguale el valor de $\frac{1}{2}n$ de los datos ordenados.
• El cuartil superior ocupa la menor posición que supere o iguale el valor de $\frac{3}{4}n$ de los datos ordenados.

3. Rango intercuartilico

El rango intercuartilico (RI) de un conjunto de datos, es la distancia entre el cuartil superior y el cuartil inferior, es decir: $$RI=Q_3-Q_1$$ Indica el intervalo central, donde se encuentra el 50% de las observaciones.

4. Pasos para la construcción de un box plot

4.1 Ordenar los datos de menor a mayor.

4.2 Calcular los cuartiles y el rango.

4.3 Calcular las cotas que permiten decidir si un dato es outlier: Segunda cota inferior = $Q_1-3RI$, primera cota inferior = $Q_1-1.5RI$, primera cota superior = $Q_3+1.5RI$ y segunda cota superior = $Q_3+3RI$

4.4 Dibujar una escala que cubra el rango de variación de los datos y marcar la mediana y los cuartiles. Dibujar una caja que se extienda entre los cuartiles y marcar en ella la posición de la mediana.

4.5 Partiendo del cuartil inferior trazar una línea (bigote) que llegue hasta el último dato contenido “dentro” de la primera cota inferior y de igual forma, partiendo del cuartil superior trazar una línea (bigote) que llegue hasta el último dato contenido “dentro” de la primera cota superior.

4.6 Clasificar los outliers, un dato que caiga entre la 1a y 2a cota inferior o entre la 1a y 2a cota superior será declarado outlier y se marca con un símbolo (por ejemplo, *). Cualquier dato que caiga por fuera de la 2a cota inferior o la 2a cota superior será declarado outlier severo y se marca con otro símbolo (por ejemplo, $\circ$).

5. Ejemplo

Consideremos los siguientes datos ordenados 

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 \\ \hline 100 & 112 & 134 & 146 & 155 & 168 & 170 & 195 & 246 & 302 & 338 & 412 & 678 \\ \hline \end{array}$$Cuartiles\begin{align}&\text{Posición del cuartil inferior en}\,\, n/4=3.25\hspace{3.9cm} Q_1=146\\&\text{Posición de la mediana en}\,\,  n/2=6.5\hspace{2cm}\Longrightarrow\hspace{2cm} Q_2=170\\&\text{Posición del cuartil superior en}\,\,3n/4=9.75\hspace{3.41cm} Q_3=302\end{align}

• Rango intercuartilico $RI=Q_3-Q_1=156$ 
• Segunda cota inferior $Q_1-3RI=-322$
• Primera cota inferior $Q_1-1.5RI=-88$ 
• Primera cota superior $Q_3+1.5RI=536$ 
• Segunda cota superior $Q_3+3RI=770$ 

Por tanto, el box plot resultante se muestra como:

Fig 2. Ejemplo de boxplot

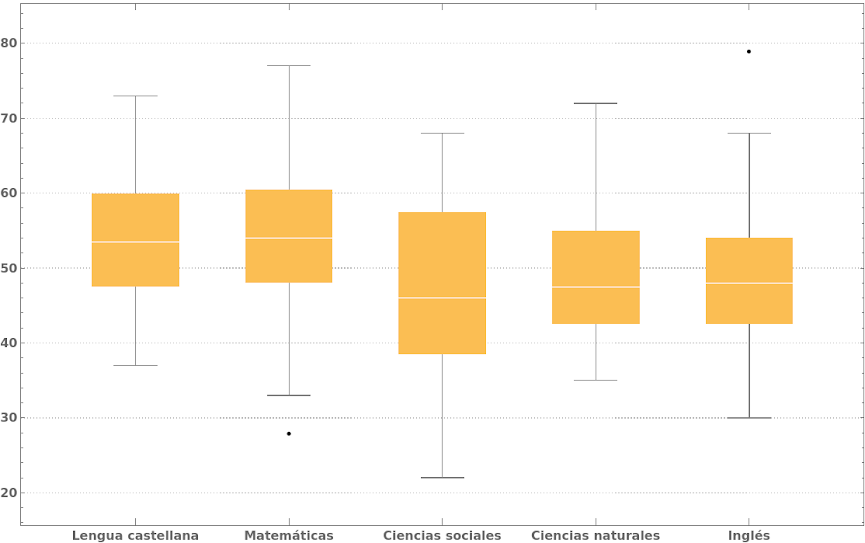
6. Aplicación del box plot en las pruebas icfes. Los resultados de las pruebas icfes 2022 de la I.E. Francisco de Miranda, se pueden ver en la siguiente sabana boxplot.

Fig 3. Boxplot de los resultados ICFES 2022

La sabana Boxplot de la Fig 3. Se obtuvo con el siguiente comando en Mathematica 13 (Lo puedes seleccionar y dar ctrl + c, abrir en mathematica 13 un nuevo documento, dar ctrl + v y dar  Shift + Enter para correr el programa)

Código en mathematica 13 para generar una sabana boxplot

LC = {53, 53, 55, 54, 69, 42, 54, 58, 51, 60, 58, 54, 61, 48, 60, 55, 47, 66, 44, 54, 49, 50, 47, 47, 40, 37, 67, 63, 53, 43, 53, 47, 40,63, 45, 47, 60, 52, 45, 42, 64, 67, 49, 49, 50, 73, 49, 63, 57,73, 65, 54, 60, 53, 41, 43, 45, 69, 58, 58, 62, 59, 67, 51, 52, 56,64, 65, 49, 38, 51, 55};

Math = {55, 57, 46, 51, 66, 52, 49, 48, 54, 56, 62, 67, 61, 54, 54, 54, 43, 64, 48, 65, 53, 47, 49, 45, 41, 52, 64, 56, 50, 37, 52, 45, 33, 59, 44, 49, 53, 59, 46, 43, 61, 70, 50, 46, 59, 77, 55, 60, 64, 67, 58, 55, 66, 65, 49, 28, 47, 64, 57, 70, 58, 56, 49, 50, 48, 61, 67, 57, 36, 40, 45, 50};

CS = {40, 46, 51, 52, 51, 41, 36, 49, 54, 54, 53, 53, 60, 38, 43, 38, 46, 62, 32, 44, 38, 41, 52, 32, 36, 22, 63, 61, 44, 39, 39, 44, 32, 62, 37, 37, 50, 45, 61, 43, 57, 61, 33, 38, 53, 61, 44, 60, 59, 67, 50, 47, 55, 45, 27, 44, 31, 68, 58, 63, 49, 65, 62, 41, 45, 48, 66, 58, 34, 27, 33, 45};

CN = {49, 45, 45, 51, 67, 44, 37, 43, 49, 46, 53, 53, 56, 45, 38, 49, 41, 72, 44, 53, 43, 50, 42, 41, 44, 38, 61, 60, 43, 42, 46, 38, 40, 49, 48, 42, 44, 51, 46, 47, 56, 59, 43, 45, 55, 65, 50, 47, 57, 64, 56, 48, 55, 58, 40, 35, 39, 63, 63, 68, 41, 57, 66, 43, 41, 49, 55, 48, 41, 37, 41, 49};

ING = {48, 50, 52, 44, 49, 36, 38, 48, 44, 68, 53, 68, 35, 43, 52, 61, 34, 67, 43, 51, 40, 47, 51, 37, 43, 47, 53, 45, 40, 52, 52, 34, 48, 67, 46, 49, 47, 51, 42, 62, 58, 48, 44, 47, 58, 65, 42, 55, 64, 79, 53, 46, 43, 62, 30, 41, 54, 63, 38, 64, 52, 57, 48, 39, 54, 48, 63, 31, 38, 38, 48, 35};

BoxWhiskerChart[Table[{LC, Math, CS, CN, ING}], "Outliers", BaseStyle -> {FontFamily -> "Arial", FontSize -> 12, FontWeight -> "Bold"}, PlotTheme -> "Detailed", ChartLabels -> {"Lengua castellana", "Matemáticas", "Ciencias sociales", "Ciencias naturales", "Inglés"}]